Here is the price chart for the last nine months for Detour Corp (DGC-T) [Disclosure: long]
Now suppose we decide we want to know something about what is driving the price of this stock. We have a time series (here we've plotted the daily closing prices for the last nine months or so). We think the dynamics of this time series might be interesting and are hopeful that if we were to learn something of them it might help us decide when or at what price we would wish to buy (or sell) this stock.
We know very little about what drives stock prices. If we were to guess at a conceptual model for the dynamics governing this particular stock price, it would probably include: the gold price; the perception of expected expenses in developing the property; the perception of political problems (native concerns or sudden mining tariffs, or somesuch); or the general perception of the overall stock market.
A sophisticated observer might want to add some stochastic element as well as something that takes into consideration the psychology of the observers interested in this particular stock. For we often observe that stock prices have a sort of momentum--when they have been stuck in a narrow range for some time, they are more likely to remain within that range, but if they break decisively, the stock price can be driven by "momentum", whether such momentum arises from investor herding or confirmation bias.
The tripping of a psychological switch allows for the prospect of some sort of feedback within our pricing system. All in all, it is beginning to look like the differential equations used to describe our system are going to end up being at least in part nonlinear. And the time series outputs from nonlinear systems are notoriously difficult to understand (or model).
So our system is affected by numeous factors, all of which we would like to at least have the potential to analyze. But all we have is price. Is it enough? Many commentators (this is not intended to endorse the services of the linked gentlemen) tell us all we have to do is watch price. But are they right?
It turns out that they are. I know, I can hardly believe it myself. I must admit I have some doubts about whether these commentators understand why price is all that matters, but also acknowledge that once you have an empirical method that works for you, you may not feel you need to understand why it works. In fact developing such an understanding may only subtract from the amount of time you have to make money.
The reason why price is all you need is one of the deep mysteries of ergodic theory. In short, all information concerning the dynamics of all the inputs is recorded in all of the outputs of a system. Price is just such an output. Equally well, you might use volume or change in price, as these will both reflect the dynamics in which we are interested; however the relative weights of each component driving the changes in price may be different for each of these time series. But the information is all present in each series, so we should not gain very much by studying price in conjunction with one of these other variables.
Now the dynamics of numerous different factors are not revealed within a one-dimensional plot, which is all the above chart really is. We have stretched out time, but had we not done so, we would have ended up with something like this.
Not much to see here. All you could really make out is the highest price (the top of the line) and the lowest price (the bottom of the line)
In order to see all the dynamics of interest, we need to "unfold" the plot of the time series into a phase space plot with enough dimensions to reveal all the dynamics of all the factors influencing it. Normally you will need at least three dimensions to really see anything interesting. More practically, the plot should never intersect itself.
One way of unfolding the data is to plot it against some other data series which is related somehow, but which can be considered independent. By this I don't mean looking at parallel line charts--I mean a scatter plot of one variable against another.
For paleoclimate studies you might plot your proxy data for global ice volume against, say, your proxy for atmospheric CO2 and/or your proxy for deep ocean temperature (e.g., Saltzman and Verbitsky, 1995).
We don't have so many variables to choose from, so let's look at the closing price plotted against daily volume for DGC. One advantage we have over the paleoclimatologists is that by definition, both of these data series are sampled at the same intervals, and we can obtain both series over the complete interval of study (the last nine months here). You won't believe how much of a problem this can be in studying natural time series.
To create the graph at right, I have plotted the daily closing price against the daily volume for each day over the last nine months. The points are plotted in chronological order, and a curved line (as per tradition) is drawn through the points.
Each plotted point is called a state, and the graph itself is called a state space (alternatively phase space is also used). The curved line represents the trajectory of the system as it evolves through time.
What we have here is a state space of sequential price-volume states for Detour Gold Corp. from late November 2009 to late August 2010.
The beginning of the plot is somewhere in the tangle near $15. There is so much action there it is hard to see. The end of the plot is easier to see--it is the tail of the graph there at middling volume and a price over $30. Interesting, but hard to interpret.
I could easily choose another data series to plot against price. This time I will plot daily price against the change in price from the previous close.
Here we actually have a plot that is easier to follow. Even though the beginning is hard to make out, there is little doubt about which way the system is evolving.
It is always moving clockwise around the loops, for the simple reason that below the horizontal axis, the price change was negative, meaning that the subsequent price is lower than the previous price.
Above the horizontal axis, the price change is positive, so the subsequent price must be higher than the previous price.
The further the curve is from the horizontal axis, the more rapid the price change. Consequently any area of stability must lie along or very close to the horizontal axis.
The above state space is very nearly a type that we would actually use. The only problem with it is that it is tilted slightly to the right, and this is because in calculating the price change, we use only a given point and the previous point. In principle, this price change should be considered valid for the middle of the trading day instead of the end. One way around this would be to calculate the price change over two consecutive trading days, and plot that against the closing price of the middle day. (So find the price change between Monday's and Wednesday's closing prices and plot that against Tuesday's closing price).
And let's divide the difference by two so we end up with an average price change over each two-day stretch.
This one is similar to the last, but a little simpler. That's because we have smoothed our first difference data somewhat.
But the overall features are the same. The system evolves as a series of clockwise overlapping loops.
Since we could have calculated the price change from the price time series, we could actually say that this is a state space which has been reconstructed entirely from the price data. This is the first trick discussed in the classic paper of Packard et al. (1980)--graphing a scatter plot of the original time series against its first (and higher) time derivatives.
Intersections are impossible in a properly reconstructed state space. The reason we have intersections in the state space reconstructions here is because we need to unfold the price function into at least three dimensions, and we have only done two (excel only allows scatter plots in two dimensions--so get to work Billy!).
This is the same method as I used to reconstruct the dust flux state space depicted on the masthead of this blog.
Were we to unfold the DGC price function into three dimensions using the method above, the third dimension would be the change of the price change (or the second time derivative of the price). If any further dimensions are required, we would use the third time derivative, then the fourth, and so on. Displaying data in more than three dimensions presents problems, but the data may still be studied using an entire toolbox of mathematical techniques which are well known (Abarbanel, 1997).
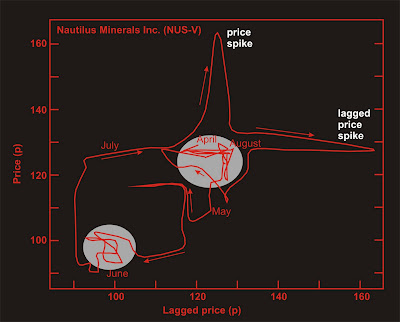
A plot of price change vs. price as we have done above is really a plot of x(n+1)-x(n) vs x(n). Could we not simplify the plot by dispensing the x(n) term on the ordinate? Can we not simply plot x(n+k) vs x(n), where k represents a lag? If we do, we end up with a plot (which is a reconstructed state space using the time-delay method) which looks a little different from the x(n+1)-x(n) vs x(n) graph (it is rotated 45 degrees, for instance), but the two plots are topologically equivalent.
In nature it is preferable for us to reconstruct the state space by the time-delay method because the errors in the second and higher dimensions will be smaller than if we reconstruct the state space using time derivatives. Arguably there is no error at all in the closing price, so it may be that there is no great advantage in using the time delay method for analyzing stock prices.
If we are going to use the time delay method, we have to decide on a value for k, which is called the lag. There are prescribed methods for doing so. Just as for a simple Cartesian graph, the x and y axes are perpendicular, so too for a good state space. The axes will be as close to orthogonal as possible if the average mutual information is a minimum. Hence the value of k chosen is the one for which the average mutual information between the time series and the lagged time series is a minimum.
Did you look at that equation? What many do instead is calculate the autocorrelation function of the time series for several lags, and choose a lag for which the absolute value of the correlation is a minimum. For many data sets, especially data sets which are almost periodic, the lag obtained in this manner will be very close to the optimum lag. Furthermore, the method is actually somewhat forgiving.
Does the time series of closing price show almost-periodic behaviour? Our graph for DGC does not appear to do so, but it is rather dominated by a long uptrend so it may be hard to say. There is reason to suppose that other stock prices may have such behaviour due to the relatively predictable recurrences of the weekend, month-end, seasonal, and year-end periods, and the periodicity may be a function of the timing of options settlement.
In the plots from the three earlier parts of this series, I have used a lag of four days. This choice was somewhat arbitrary. In the next part we will look at the DGC data with several different lags.
Now suppose we decide we want to know something about what is driving the price of this stock. We have a time series (here we've plotted the daily closing prices for the last nine months or so). We think the dynamics of this time series might be interesting and are hopeful that if we were to learn something of them it might help us decide when or at what price we would wish to buy (or sell) this stock.
We know very little about what drives stock prices. If we were to guess at a conceptual model for the dynamics governing this particular stock price, it would probably include: the gold price; the perception of expected expenses in developing the property; the perception of political problems (native concerns or sudden mining tariffs, or somesuch); or the general perception of the overall stock market.
A sophisticated observer might want to add some stochastic element as well as something that takes into consideration the psychology of the observers interested in this particular stock. For we often observe that stock prices have a sort of momentum--when they have been stuck in a narrow range for some time, they are more likely to remain within that range, but if they break decisively, the stock price can be driven by "momentum", whether such momentum arises from investor herding or confirmation bias.
The tripping of a psychological switch allows for the prospect of some sort of feedback within our pricing system. All in all, it is beginning to look like the differential equations used to describe our system are going to end up being at least in part nonlinear. And the time series outputs from nonlinear systems are notoriously difficult to understand (or model).
So our system is affected by numeous factors, all of which we would like to at least have the potential to analyze. But all we have is price. Is it enough? Many commentators (this is not intended to endorse the services of the linked gentlemen) tell us all we have to do is watch price. But are they right?
It turns out that they are. I know, I can hardly believe it myself. I must admit I have some doubts about whether these commentators understand why price is all that matters, but also acknowledge that once you have an empirical method that works for you, you may not feel you need to understand why it works. In fact developing such an understanding may only subtract from the amount of time you have to make money.
The reason why price is all you need is one of the deep mysteries of ergodic theory. In short, all information concerning the dynamics of all the inputs is recorded in all of the outputs of a system. Price is just such an output. Equally well, you might use volume or change in price, as these will both reflect the dynamics in which we are interested; however the relative weights of each component driving the changes in price may be different for each of these time series. But the information is all present in each series, so we should not gain very much by studying price in conjunction with one of these other variables.
Now the dynamics of numerous different factors are not revealed within a one-dimensional plot, which is all the above chart really is. We have stretched out time, but had we not done so, we would have ended up with something like this.
Not much to see here. All you could really make out is the highest price (the top of the line) and the lowest price (the bottom of the line)
In order to see all the dynamics of interest, we need to "unfold" the plot of the time series into a phase space plot with enough dimensions to reveal all the dynamics of all the factors influencing it. Normally you will need at least three dimensions to really see anything interesting. More practically, the plot should never intersect itself.
One way of unfolding the data is to plot it against some other data series which is related somehow, but which can be considered independent. By this I don't mean looking at parallel line charts--I mean a scatter plot of one variable against another.
For paleoclimate studies you might plot your proxy data for global ice volume against, say, your proxy for atmospheric CO2 and/or your proxy for deep ocean temperature (e.g., Saltzman and Verbitsky, 1995).
We don't have so many variables to choose from, so let's look at the closing price plotted against daily volume for DGC. One advantage we have over the paleoclimatologists is that by definition, both of these data series are sampled at the same intervals, and we can obtain both series over the complete interval of study (the last nine months here). You won't believe how much of a problem this can be in studying natural time series.
To create the graph at right, I have plotted the daily closing price against the daily volume for each day over the last nine months. The points are plotted in chronological order, and a curved line (as per tradition) is drawn through the points.
Each plotted point is called a state, and the graph itself is called a state space (alternatively phase space is also used). The curved line represents the trajectory of the system as it evolves through time.
What we have here is a state space of sequential price-volume states for Detour Gold Corp. from late November 2009 to late August 2010.
The beginning of the plot is somewhere in the tangle near $15. There is so much action there it is hard to see. The end of the plot is easier to see--it is the tail of the graph there at middling volume and a price over $30. Interesting, but hard to interpret.
I could easily choose another data series to plot against price. This time I will plot daily price against the change in price from the previous close.
Here we actually have a plot that is easier to follow. Even though the beginning is hard to make out, there is little doubt about which way the system is evolving.
It is always moving clockwise around the loops, for the simple reason that below the horizontal axis, the price change was negative, meaning that the subsequent price is lower than the previous price.
Above the horizontal axis, the price change is positive, so the subsequent price must be higher than the previous price.
The further the curve is from the horizontal axis, the more rapid the price change. Consequently any area of stability must lie along or very close to the horizontal axis.
The above state space is very nearly a type that we would actually use. The only problem with it is that it is tilted slightly to the right, and this is because in calculating the price change, we use only a given point and the previous point. In principle, this price change should be considered valid for the middle of the trading day instead of the end. One way around this would be to calculate the price change over two consecutive trading days, and plot that against the closing price of the middle day. (So find the price change between Monday's and Wednesday's closing prices and plot that against Tuesday's closing price).
And let's divide the difference by two so we end up with an average price change over each two-day stretch.
This one is similar to the last, but a little simpler. That's because we have smoothed our first difference data somewhat.
But the overall features are the same. The system evolves as a series of clockwise overlapping loops.
Since we could have calculated the price change from the price time series, we could actually say that this is a state space which has been reconstructed entirely from the price data. This is the first trick discussed in the classic paper of Packard et al. (1980)--graphing a scatter plot of the original time series against its first (and higher) time derivatives.
Intersections are impossible in a properly reconstructed state space. The reason we have intersections in the state space reconstructions here is because we need to unfold the price function into at least three dimensions, and we have only done two (excel only allows scatter plots in two dimensions--so get to work Billy!).
This is the same method as I used to reconstruct the dust flux state space depicted on the masthead of this blog.
Were we to unfold the DGC price function into three dimensions using the method above, the third dimension would be the change of the price change (or the second time derivative of the price). If any further dimensions are required, we would use the third time derivative, then the fourth, and so on. Displaying data in more than three dimensions presents problems, but the data may still be studied using an entire toolbox of mathematical techniques which are well known (Abarbanel, 1997).
A plot of price change vs. price as we have done above is really a plot of x(n+1)-x(n) vs x(n). Could we not simplify the plot by dispensing the x(n) term on the ordinate? Can we not simply plot x(n+k) vs x(n), where k represents a lag? If we do, we end up with a plot (which is a reconstructed state space using the time-delay method) which looks a little different from the x(n+1)-x(n) vs x(n) graph (it is rotated 45 degrees, for instance), but the two plots are topologically equivalent.
In nature it is preferable for us to reconstruct the state space by the time-delay method because the errors in the second and higher dimensions will be smaller than if we reconstruct the state space using time derivatives. Arguably there is no error at all in the closing price, so it may be that there is no great advantage in using the time delay method for analyzing stock prices.
If we are going to use the time delay method, we have to decide on a value for k, which is called the lag. There are prescribed methods for doing so. Just as for a simple Cartesian graph, the x and y axes are perpendicular, so too for a good state space. The axes will be as close to orthogonal as possible if the average mutual information is a minimum. Hence the value of k chosen is the one for which the average mutual information between the time series and the lagged time series is a minimum.
Did you look at that equation? What many do instead is calculate the autocorrelation function of the time series for several lags, and choose a lag for which the absolute value of the correlation is a minimum. For many data sets, especially data sets which are almost periodic, the lag obtained in this manner will be very close to the optimum lag. Furthermore, the method is actually somewhat forgiving.
Does the time series of closing price show almost-periodic behaviour? Our graph for DGC does not appear to do so, but it is rather dominated by a long uptrend so it may be hard to say. There is reason to suppose that other stock prices may have such behaviour due to the relatively predictable recurrences of the weekend, month-end, seasonal, and year-end periods, and the periodicity may be a function of the timing of options settlement.
In the plots from the three earlier parts of this series, I have used a lag of four days. This choice was somewhat arbitrary. In the next part we will look at the DGC data with several different lags.